Queen's Attack II HackerRank Solution in Java with Explanation

Queen's Attack II Problem's Solution in Java (Chessboard Problem)

 

Problem Description :

You will be given a square chess board with one queen and a number of obstacles placed on it. Determine how many squares the queen can attack. 

A queen is standing on an n * n chessboard. The chess board's rows are numbered from 1 to n, going from bottom to top. Its columns are numbered from 1 to n, going from left to right. Each square is referenced by a tuple, (r, c), describing the row r and column c, where the square is located.

The queen is standing at position (r_q, c_q). In a single move, queen can attack any square in any of the eight directions

The queen can move:

1. Horizontally (left, right)
2. Vertically (up, down)
3. Diagonally (four directions: up-left, up-right, down-left, down-right)

The queen can move any number of squares in any of these directions, but it cannot move through obstacles.

Input Format :

• n : The size of the chessboard (n x n).
• k : The number of obstacles.
• r_q and c_q : The row and column coordinates of the queen.
• obstacles : An array of obstacle coordinates (r_i and c_i) where each obstacle is located.

Output :

• The number of squares the queen can attack.
  

Solution : Queen's Attack Chess board Problem Solution in Java

import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;

public class QueensAttackII {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        
        System.out.println("Enter the size of the chessboard (n):");
        int n = scanner.nextInt();
        
        System.out.println("Enter the number of obstacles (k):");
        int k = scanner.nextInt();
        
        System.out.println("Enter the row coordinate of the queen (r_q):");
        int r_q = scanner.nextInt();
        
        System.out.println("Enter the column coordinate of the queen (c_q):");
        int c_q = scanner.nextInt();
        
        System.out.println("Enter the coordinates of obstacles (r_i and c_i):");
        int[][] obstacles = new int[k][2];
        for (int i = 0; i < k; i++) {
            obstacles[i][0] = scanner.nextInt();
            obstacles[i][1] = scanner.nextInt();
        }
        
        int result = queensAttack(n, k, r_q, c_q, obstacles);
        System.out.println("Number of squares the queen can attack: " + result);
        
    }
    
    static int queensAttack(int n, int k, int r_q, int c_q, int[][] obstacles) {
        int totalAttackedSquares = 0;
        
        // Calculate the directions in which the queen can move
        int[][] directions = {
            {0, 1},   // Right
            {0, -1},  // Left
            {1, 0},   // Down
            {-1, 0},  // Up
            {-1, 1},  // Up-right
            {-1, -1}, // Up-left
            {1, 1},   // Down-right
            {1, -1}   // Down-left
        };
        
        // Create a set to store the obstacle positions in Set of string for efficient lookup
        Set<String> obstacleSet = new HashSet<>();
        for (int[] obstacle : obstacles) {
            obstacleSet.add(obstacle[0] + "-" + obstacle[1]);
        }
        
        // Check each direction and count the attacked squares
        for (int[] direction : directions) {
            int row = r_q + direction[0];
            int col = c_q + direction[1];
            
            while (row >= 1 && row <= n && col >= 1 && col <= n) {
                String position = row + "-" + col;
                
                // Stop if there's an obstacle in this direction
                if (obstacleSet.contains(position)) {
                    break;
                }
                
                totalAttackedSquares++;
                row += direction[0];
                col += direction[1];
            }
        }
        
        return totalAttackedSquares;
    }

}

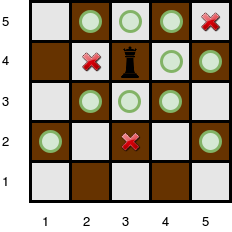
Input 1 :

5 row and 5 column, 3 obstacles
    5 3
queen's position in chessboard 
    4 3
obstacles rows and columns location in chessboard
    5 5   
    4 2
    2 3 

Output 1 :

10

The queen is standing at position (4, 3) on (5, 5) chessboard with k = 3 obstacles.

Input 2 :

1 row and 1 column, 0 obstacles
    1 0
queen's position in chessboard 
    1 1

Output 2 :

0

Since there is only one square, and the queen is on it, the queen can move 0 squares.

 

Explanation of Code :

    int totalAttackedSquares = 0;

    int[][] directions = {
        {0, 1},   // Right
        {0, -1},  // Left
        {1, 0},   // Down
        {-1, 0},  // Up
        {-1, 1},  // Up-right
        {-1, -1}, // Up-left
        {1, 1},   // Down-right
        {1, -1}   // Down-left
    };

Initialize a variable totalAttackedSquares to keep track of the total number of squares the queen can attack.

Define an array called directions to represent the eight possible directions in which the queen can move. Each direction is represented as an array of two integers, where the first element represents the change in the row, and the second element represents the change in the column.

    Set<String> obstacleSet = new HashSet<>();
    for (int[] obstacle : obstacles) {
        obstacleSet.add(obstacle[0] + "-" + obstacle[1]);
    }

Create a HashSet called obstacleSet to efficiently store the positions of obstacles on the chessboard.  Next Iterate through the obstacles array (Given in parameters) and add each obstacle's position (in the format "row-column") to the set. This will allow us to quickly check if a given square contains an obstacle.

    for (int[] direction : directions) {
        int row = r_q + direction[0];
        int col = c_q + direction[1];
        
        while (row >= 1 && row <= n && col >= 1 && col <= n)

First loop through each of the eight possible directions in which the queen can move.

Then initialize row and col to represent the next square the queen would move to in the current direction.

     String position = row + "-" + col;

     if (obstacleSet.contains(position)) {
         break; // Stop if there's an obstacle in this direction
     }

     totalAttackedSquares++;
     row += direction[0];
     col += direction[1];
 

create a string called position to represent the current square's position in the "row-column" format.

check if the obstacleSet contains the current position. If it does, then break out of the loop because the queen cannot move beyond an obstacle in this direction.

If there's no obstacle in the current direction, we increment totalAttackedSquares because the queen can attack this square.

Finally, update the row and col values to move to the next square in the same direction and continue the loop.

Return totalAttackedSquares.

 

Happy Coding..

Other Coding Problem's and its Solutions :

• Find Non-Divisible Subset from Given Array 
• Check if two strings after processing backspace character are equal or not  
• Java Program for Search an element in Rotated Sorted Array
• Find First and Last Position of Element in Sorted Array with Explanation